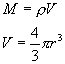
Die physikalischen Größen der Sterne wie Temperatur, Masse, mittlere Dichte lassen sich
grundsätzlich nur indirekt messen.
Erst recht gilt dies für die physikalischen Eigenschaften aus dem direkt überhaupt nicht mehr zugänglichen Sterninneren.
Dieser Beitrag soll grundsätzlich zeigen, wie man zu einem physikalisch
fundierten Modell über den inneren Aufbau einer Gaskugel kommt. Der Einfachheit halber soll hier ein rein
mechanisches Sternmodell untersucht werden. Mit dieser Frage hat sich R. Emden 1907 ausführlich
beschäftigt. Kurzbiografie
vom Emden.
Die Frage der Energieerzeugung wird dabei ausgespart, wohl wissend, dass damit ein ganz wesentlicher
Gesichtspunkt vernachlässigt wird. Aber grundsätzlich ist dies ein typisches Kennzeichen mathematisch-physikalischer
Modelle, dass nämlich bestimmte Annahmen und Vereinfachungen gemacht werden, sei es, dass genauere
Grundlagen fehlen oder aber ein Modell erst durch solche Annahmen lösbar wird.
Computer sind sehr hilfreich bei der numerischen Rechnung (in vielen Fällen wird die numerische Rechnung
überhaupt erst möglich), ersetzen aber nicht ein genau durchdachtes Modell!
Der Einfachheit halber nehmen wir einen kugelsymmetrischen Aufbau an, die Dichte ρ sei also nur eine Funktion des Abstandes vom Kugelmittelpunkt r. Diese Annahme ist bei einer Kugel "vernünftig", denn wenn die Kugel nicht rotiert und keine weiteren äußeren Kräfte wirksam sind, gibt es keinen Grund für einen anderen Ansatz.
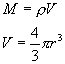 |
(1) |
Obige Gleichung für die Masse M lässt sich natürlich nur anwenden bei konstanter Dichte oder bei bekannter
mittlerer Dichte. Um eine Aussage über die Dichte in Abhängigkeit vom Zentrum zu erhalten, muss
etwas mehr Mathematik betrieben werden. Man kann sich nämlich die Kugel aus sehr vielen Kugelschalen aufgebaut denken, wobei die
Schalen so dünn sein sollten, dass man die Dichte für eine Schale als konstant betrachten kann.
Das Masse einer solchen Kugelschale ergibt sich nach
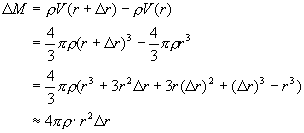 |
Wir finden also für die Änderung der Masse in Abhängigkeit vom Radius die Beziehung:
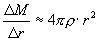 |
bzw. in der Schreibweise der Differentialrechnung (Δr geht gegen 0, wird also beliebig klein):
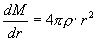 |
(2) |
Diese Differentialgleichung beschreibt ohne jede Näherung oder Zusatzannahme die Änderung der Masse in Abhängigkeit von der Entfernung vom Zentrum und ist eine der grundlegenden Gleichungen des Sternaufbaus.
Die Gaskugel soll sich im Gleichgewicht befinden, das heißt, die durch die Gravitation verursachte Kraft auf ein beliebiges Gebiet im Sterninneren muss durch den dort wirkenden Gasdruck kompensiert werden. Man erhält eine Differentialgleichung, die die Änderung des Druckes in Abhängigkeit von der Entfernung vom Zentrum beschreibt. Ohne Ableitung soll hier nur das Ergebnis stehen.
 |
(3) |
Die beiden Gleichungen sind zwei der Grundgleichungen des Sternaufbaus. Eine Lösung ist jedoch nicht eindeutig möglich, denn zwei Gleichungen stehen drei Unbekannte gegenüber (M, P und ρ). Weiterhin müssen die Anfangsbedingungen für r = 0 erfüllt sein:
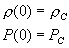 |
(4) |
Dies sind genau die Dichte und der Druck im Zentrum der Gaskugel, also Größen, die zunächst vollkommen
unbekannt sind. Deshalb kann man auch die beiden Ausgangsgleichungen nicht einfach integrieren
Zur Lösung benötigen wir noch eine Beziehung zwischen dem Druck und der Dichte des Gases.
Genau dies leistet die sog. "Polytrope Zustandsgleichung".
Sie stellt einen Zusammenhang zwischen Gasdruck und der Dichte her. Beide Größen hängen im Stern natürlich von Abstand zum Zentrum ab.
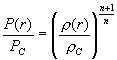 |
(5) |
Die Schreibweise des Exponenten wird sich später als vorteilhaft herausstellen. Der Term (n+1)/n stellt nichts anderes dar als irgendeinen Bruch ungleich eins. Jeder Bruch der Form a/b läßt sich nämlich in dieser Form darstellen mit n = b/(a-b).
Wir definieren zunächst eine Hilfsfunktion F
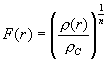 |
(5) |
Die Dichte und der Druck als Funktionen vom Abstand lassen sich unter Verwendung der Hilfsfunktion F schreiben als:
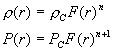 |
(6) |
Wir haben das Problem der Dichte- und Druckfunktion reduziert auf die Bestimmung einer Hilfsfunktion F, mit deren Kenntnis Druck und Dichte für jeden Abstand vom Zentrum berechnet werden können. Die Bestimmung von F erfordert - was sehr wichtig ist - keinerlei Kenntnis der zentralen Dichte oder des Druckes im Zentrum.
Die beiden Ausgangsdifferentialgleichungen lassen sich unter Benutzung von F umformen und nach einiger Rechnung und Einführung einer neuen Unabhängigen x (die proportional zu r ist) erhält man die sog. Lane-Emden-Gleichung, eine nichtlineare Differentialgleichung zweiter Ordnung:
 |
(10) |
mit den Anfangsbedingungen:
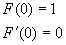 |
Diese Gleichung hat nur für wenige Werte von n eine geschlossene (formelmäßige) Lösung. Um die
Lane-Emden-Gleichung numerisch zu lösen, ist es zweckmäßig, die Differentialgleichung zweiter Ordnung
in zwei Differentialgleichungen erster Ordnung (es treten dort nur erste Ableitungen auf) umzuwandeln.
Für die Lösung eines derartigen Systems von gewöhnlichen Diffenrentialgleichungen existieren leicht
anwendbare numerische Verfahren, die hier nicht weiter erörtert werden können.
Löst man nun mit geeigneten Methoden dieses System, so muss die Rechnung abgebrochen werden, wenn
F kleiner als Null wird, da die Potenz einer negativen Zahl mit nichtganzzahligen Exponenten nicht
definiert ist und hier physikalisch gesehen die "Oberfläche" der Gaskugel erreicht ist (und damit auch die Grenze des
Modells).
Die mittlere Dichte ρm die Dichte im Zentrum ρc sowie der Druck im Zentrum Pc
können jetzt - hier ohne weitere Begründung - über die Beziehungen
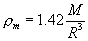 |
in g/cm3 | (7) |
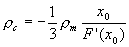 |
in g/cm3 | (8) |
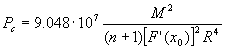 |
in MPa | (9) |
berechnet werden. x0 ist hierbei die Nullstelle der Funktion F.
Die numerische Integration der Gleichung (10) gelingt mit einfachen Mitteln, es genügt hier beispielsweise das klassische Runge-Kutta-Verfahren. Beispielhaft sollen hier die Ergebnisse für zwei Modellrechnungen dargestellt werden. Die Masse sei M = 2·MSonne, und der Radius R = 3·RSonne. Wir nehmen zwei verschiedene Polytropenindizes an: In den Abbildungen sind die Funktionen F(x) und ihre Ableitung F'(x) für zwei Polytropenindizes dargestellt.
| Polytropenindex = 1,5 | Polytropenindex = 3,0 |
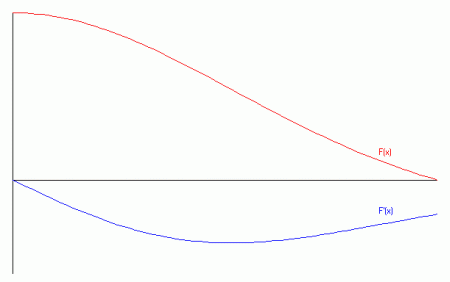 | 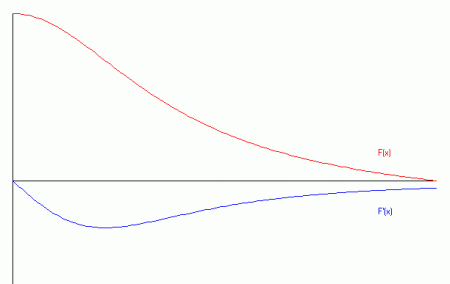 |
| Graphen der Funktionen F(x) und F'(x) | Graphen der Funktionen F(x) und F'(x) |
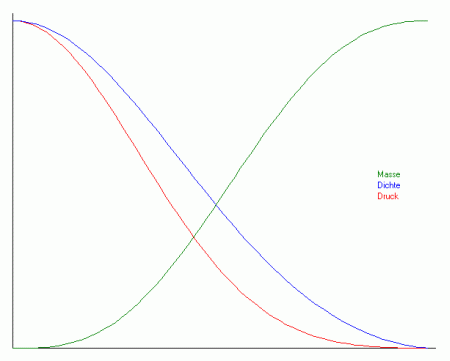 | 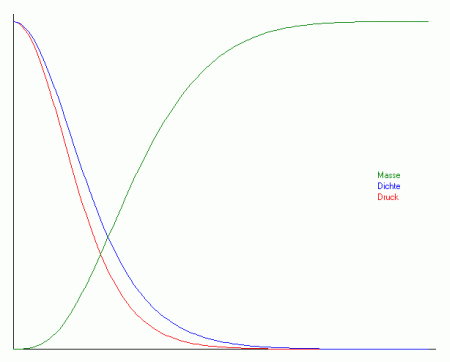 |
| Graphen für Masse, Dichte und Druck in Abhängigkeit von x (normiert auf das jeweilige Maximum) |
Graphen für Masse, Dichte und Druck in Abhängigkeit von x (normiert auf das jeweilige Maximum) |
| |
|
| physikalische Daten im Zentrum: Druck: 4,3·107 MPa Dichte: 0,63 g/cm3 |
physikalische Daten im Zentrum: Druck: 6,2·108 MPa Dichte: 5,7 g/cm3 |
Man sieht in den Bildern, dass die Funktionen umso steiler verlaufen, je größer der Polytropenindex ist. Dies kann man nach den Gleichungen (6) auch erwarten. Die Werte im Zentrum nehmen mit höheren Polytropenindizes ebenfalls zu. Man sieht weiterhin, dass der Druck im Verhältnis stärker abfällt als die Dichte.